True Search Engines Parser. Search Engine Parser

True Search Engines Parser. Search Engine Parser

"If it is a search engine, then it can be parsed" - some random guy

search-engine-parser is a package that lets you query popular search engines and scrape for result titles, links, descriptions and more. It aims to scrape the widest range of search engines. View all supported engines

Popular Supported Engines

Popular search engines supported include:

• Google
• DuckDuckGo
• GitHub
• StackOverflow
• Baidu
• YouTube

View all supported engines here.

Installation

Install from PyPi:

# install only package dependencies pip install search-engine-parser # Installs `pysearch` cli tool pip install "search-engine-parser"

or from master:

pip install git+https://github.com/bisoncorps/search-engine-parser

Development

Clone the repository:

git clone:bisoncorps/search-engine-parser.git

Then create a virtual environment and install the required packages:

mkvirtualenv search_engine_parser pip install -r requirements/dev.txt

Code Documentation

Code docs can be found on.

Running the tests

pytest

Usage

Code

Query results can be scraped from popular search engines, as shown in the example snippet below.

Parsing in Artificial Intelligence. A Simple Artificial Intelligence Capable of Basic Reading Comprehension

I was interested in an artificial intelligence that could do reading comprehension, but surprisingly, I could not find much on the topic. I decided to try and create an AI that could do some basic reading comprehension and I got some good results:

Short Passage (Input):
Mary went sledding with her family. Mary won a race against her brother to the bottom of a hill. Mary cheered because it was her first time winning.

Input: Where did Mary go?
Output: Sledding

Input: What did Mary win?
Output: A race
Input: Who did Mary win a race against?
Output: Her brother

Input: Where did Mary win a race to?
Output: The bottom of the hill
Input: Why did Mary cheer?
Output: Because it was her first time winning

As we can see, the program can actually answer the questions about the passage.

Full Source Available Here

Introduction

What I am trying to accomplish is program capable of artificial semantic memory . Semantic memory refers to how we store our explicit knowledge and facts about the world. For example, our memory of our birth date or our knowledge that humans are mammals. I wanted to be able to make something that was able to read a passage and answer any questions I had.

Abstract Idea

An abstract idea of how I accomplished artificial semantic memory was to create a structure that can store a sentence in a different way that can be used to answer questions.

1. Structure the relationships betweens objects (nouns) in the sentence.

For example, in the sentence “Mary went sledding with her family”, there are three objects “Mary”, “sledding” and “her family”. Mary has a verb “go” (present tense of went) with the object “sledding”. The verb “go” is “with” the object “her parents”.

After brainstorming different ways to represent the relationships between objects and actions, I came up with a structure similar to a trie which I will call a “word graph”. In a word graph, each word is a node and the edges are actions or propositions.

Examples:

Mary went sledding with her family

Mary won a race against her brother to the bottom of the hill

Mary cheered because it was her first time winning

2. Answer questions using the structure.

A key observation to answering questions is that they can be reworded to be fill in the blanks.

Role of Parser in compiler design. What is Parser (Syntax analysis)? Error Handling and Recovery in Syntax Analyzer

Syntax analysis is the second phase of compiler.

Syntax analysis is also known as parsing.

In addition to construction of the parse tree, syntax analysis also checks and reports syntax errors accurately.

(eg.)

C = a + b * 5

Syntax tree can be given as,

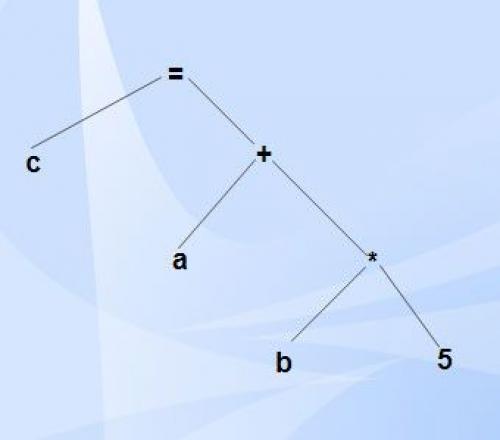
Parser is a program that obtains tokens from lexical analyzer and constructs the parse tree which is passed to the next phase of compiler for further processing.

Parser implements context free grammar for performing error checks.

We’ll be covering the following topics in this tutorial:

Types of Parser

• Top down parsers Top down parsers construct parse tree from root to leaves.

• Bottom up parsers Bottom up parsers construct parse tree from leaves to root.

Role of Parser

Figure depicts the role of parser with respect to other phases.

• It calls the function getNextToken(), to notify the lexical analyzer to yield another token.

• It scans the token one at a time from left to right to construct the parse tree.

• It also checks the syntactic constructs of the grammar.

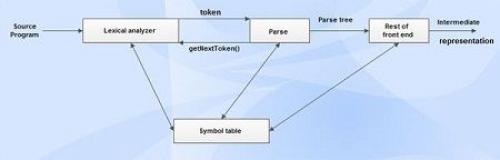
Need for Parser

• Parser is needed to detect syntactic errors efficiently.

• Error is detected as soon as a prefix of the input cannot be completed to form a string in the language. This process of analyzing the prefix of input is called viable-prefix property.

Error Recovery Strategies

Panic Mode Recovery

Synchronizing tokens are delimiters, semicolon or } whose role in source program is clear.

Context free Grammar in Artificial Intelligence. Title: Physics of Language Models: Part 1, Context-Free Grammar

Abstract: We design experiments to study $\textit{how}$ generative language models, like GPT, learn context-free grammars (CFGs) -- diverse language systems with a tree-like structure capturing many aspects of natural languages, programs, and human logics. CFGs are as hard as pushdown automata, and can be ambiguous so that verifying if a string satisfies the rules requires dynamic programming. We construct synthetic data and demonstrate that even for very challenging CFGs, pre-trained transformers can learn to generate sentences with near-perfect accuracy and remarkable $\textit{diversity}$.
More importantly, we delve into the $\textit{physical principles}$ behind how transformers learns CFGs. We discover that the hidden states within the transformer implicitly and $\textit{precisely}$ encode the CFG structure (such as putting tree node information exactly on the subtree boundary), and learn to form "boundary to boundary" attentions that resemble dynamic programming. We also cover some extension of CFGs as well as the robustness aspect of transformers against grammar mistakes. Overall, our research provides a comprehensive and empirical understanding of how transformers learn CFGs, and reveals the physical mechanisms utilized by transformers to capture the structure and rules of languages.

What is a Parser. Different Types of Parsing Algorithms

Writing a parsing algorithm is a bit like an artistic effort. In fact, if you google or maybe search on GitHub, you will find thousands of programmers who have made their own domain-specific parser. The logic and the algorithms of these Parsers do not basically follow any pattern.

Even though you can create a parser from scratch and without knowing much theory, that is not how you should do it . Science and theory exist for a good reason: to guide scientists as well as engineers and practitioners. That’s just my opinion, of course.

Thus, instead of jumping right away into writing some code that may or may not work eventually, I always try to take my time to research the problem and see what the state of the art is.

In the case of Grammar Parsing Algorithms, it turns out that the state of the art algorithms are pretty solid and widely used for a very big class of grammars (more on this last point in a minute).

Let me say it again, in different words:

You should really avoid to write a parser without first studying and understanding the basic parsing patterns that are used in the most famous compilers.

Thus, to understand and to study these algorithms is what we are about to do!

A first classification

Books and theoreticians divide parsing algorithms in two very large groups, at first. I think knowing such a definition is extremely useful: imagine yourself talking with a colleague about some piece of code. Then, you both can use this common language to understand what each is saying to the other.

This first classification is based on how the algorithm builds the parse tree in the internal memory.

First of all, let me repeat the concept: parsers build a so-called parse tree , which is a tree-like data structure whose leaves are the terminal tokens of the grammar, and the intermediate nodes in the tree are nonterminal tokens. Why a tree? This is a very good question, but let me skip it for a minute, and take it back later. Just assume we really want to have it in a tree-like shape.

If you think about a tree-like data structure, there are two sensible ways to build it. One is from the top (root) to the bottom (leaf), and the other is vice versa.

And indeed, parsing algorithms are classified in first instance as:

• Top-down Parsers,
• Bottom-up Parsers.

What does it mean in practice? Well, remember that parsing algorithms works on the grammar definition. Thus, a top-down parser will assume that the first token it sees in the input string is the start symbol of the grammar. Then, it will derive all the other tokens as children of the start symbol.

Bottom-up parsers follow the inverse logic. They will assume the first symbol seen in the input string is a leaf of the tree, and will start building the tree by deciding what is the parent node of that leaf, and so on until they arrive at the root of the tree.

This very simple classification is actually extremely important. In fact, top-down and bottom-up parsers are not different “just” in the way they build the tree. They can actually “do” different things.

In particular, and this is a very important thing to remember, bottom-up algorithms are more powerful, but also much more complex .

What does “more powerful” mean? It means that they can work with a larger set of grammars.

For example, top-down parsers do not work with left-recursive grammar, whereas bottom-up ones do. Left-recursive grammars are those grammars where a production rule for a nonterminal symbol A starts with the same symbol. For example the production rule

A : Ab

would make a grammar left-recursive, because to “replace” the symbolAin a string you have to start with another b).

We will see in a minute why top-down parsers get into trouble in such cases.

A second classification

The second classification is based on how the algorithm expands the nodes in the parse-tree .

Generally speaking, expanding a node in a tree means to figure out what are its connections (for example, its children if you are building the tree top-down). In a parse tree this means to understand what production rule must be applied to that node . Let me give a concrete example.

Let’s say we are just starting off the parsing procedure, and want to do it with a top-down approach. Therefore, we would have only one node in the tree, the root, with the start symbol of the grammar. Let’s say this symbol isS.

The grammar is likely to have many production rules for the starting symbolS, for example

S : aAb | Ac | dB.

Explain Top-Down Parsing. Top-down Parsing explained

Top-down parsing in computer science is a parsing strategy where one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar . LL parser s are a type of parser that uses a top-down parsing strategy.

Top-down parsing is a strategy of analyzing unknown data relationships by hypothesizing general parse tree structures and then considering whether the known fundamental structures are compatible with the hypothesis. It occurs in the analysis of both natural language s and computer language s.

Top-down parsing can be viewed as an attempt to find left-most derivations of an input-stream by searching for parse-trees using a top-down expansion of the given formal grammar rules. Inclusive choice is used to accommodate ambiguity by expanding all alternative right-hand-sides of grammar rules.

Simple implementations of top-down parsing do not terminate for left-recursive grammars, and top-down parsing with backtracking may have exponential time complexity with respect to the length of the input for ambiguous CFGs . which do accommodate ambiguity and left recursion in polynomial time and which generate polynomial-sized representations of the potentially exponential number of parse trees.

Programming language application

A compiler parses input from a programming language to an internal representation by matching the incoming symbols to production rules. Production rules are commonly defined using Backus–Naur form . An LL parser is a type of parser that does top-down parsing by applying each production rule to the incoming symbols, working from the left-most symbol yielded on a production rule and then proceeding to the next production rule for each non-terminal symbol encountered. In this way the parsing starts on the Left of the result side (right side) of the production rule and evaluates non-terminals from the Left first and, thus, proceeds down the parse tree for each new non-terminal before continuing to the next symbol for a production rule.

For example:

which produces the string A = acdf

would match

and attempt to matchnext. Thenwould be tried. As one may expect, some languages are more ambiguous than others. For a non-ambiguous language, in which all productions for a non-terminal produce distinct strings, the string produced by one production will not start with the same symbol as the string produced by another production. A non-ambiguous language may be parsed by an LL(1) grammar where the (1) signifies the parser reads ahead one token at a time. For an ambiguous language to be parsed by an LL parser, the parser must lookahead more than 1 symbol, e.g. LL(3).

The common solution to this problem is to use an LR parser , which is a type of shift-reduce parser , and does bottom-up parsing .

Accommodating left recursion in top-down parsing

A formal grammar that contains left recursion cannot be parsed by a naive recursive descent parser unless they are converted to a weakly equivalent right-recursive form. However, recent research demonstrates that it is possible to accommodate left-recursive grammars (along with all other forms of general CFGs ) in a more sophisticated top-down parser by use of curtailment. A recognition algorithm that accommodates ambiguous grammar s and curtails an ever-growing direct left-recursive parse by imposing depth restrictions with respect to input length and current input position, is described by Frost and Hafiz in 2006.That algorithm was extended to a complete parsing algorithm to accommodate indirect (by comparing previously computed context with current context) as well as direct left-recursion in polynomial time, and to generate compact polynomial-size representations of the potentially exponential number of parse trees for highly ambiguous grammars by Frost, Hafiz and Callaghan in 2007.

Context free and transformational Grammar in ai. Context free grammars

In this section, we present a more formal treatment of context-free grammars. In the following section, we’ll elucidate the main ideas with an example.

A language is a set of strings . Each string is a sequence of terminal symbols . In figure 3 these correspond to individual words, but more generally they may be abstract tokens . The set of terminals $\Sigma=\{\mbox{a,b,c},\ldots\}$ is called an alphabet or lexicon . There is also a set $\mathcal{V}=\{\mbox{A,B,C}\ldots…\}$ of non-terminals , one of which is the special start symbol $S$.

Finally, there are a set $\mathcal{R}$ of production or re-write rules. These relate the non-terminal symbols to each other and to the terminals. Formally, these grammar rules are a subset of the finite relation $\mathcal{R}\in \mathcal{V} \times (\Sigma \cup \mathcal{V})^*$ where $*$ denotes the. Informally, this means that each grammar rule is an ordered pair where the first element is a non-terminal from $\mathcal{V}$ and the second is any possible string containing terminals from $\Sigma$ and non-terminal from $\mathcal{V}$. For example, B$\rightarrow$ab, C$\rightarrow$Baa and A$\rightarrow$AbCa are all production rules.

A context free grammar is the tuple $G=\{\mathcal{V}, \Sigma, \mathcal{R}, S\}$ consisting of the non-terminals $\mathcal{V}$, terminals $\Sigma$, production rules $\mathcal{R}$, and start symbol $S$. The associated context-free language consists of all possible strings of terminals that are derivable from the grammar.

Informally, the term context-free means that each production rule starts with a single non-terminal symbol. Context-free grammars are part of the Chomsky hierarchy of languages which contains (in order of increasing expressiveness) regular, context-free, context-sensitive, and recursively enumerable grammars. Each differs in the family of production rules that are permitted and the complexity of the associated parsing algorithms (table 1). As we shall see, context-free languages can be parsed in $O(n^{3})$ time where $n$ is the number of observed terminals. Parsing more expressive grammars in the Chomsky hierarchy has exponential complexity. In fact, context-free grammars are not considered to be expressive enough to model real languages. Many other types of grammar have been invented that are both more expressive and parseable in polynomial time, but these are beyond the scope of this post.

Language	Recognizer	Parsing Complexity
Recursively enumerable Context-sensitiveContext-freeRegular	Turing machineLinear-bounded automata Pushdown automataFinite-state automata	decideablePSPACE$O(n^3)$$O(n)$

Table 1. The Chomsky hierarchy of languages. As the grammar-type becomes simpler, the required computation model (recognizer) becomes less general and the parsing complexity decreases.

Top-Down Parser in ai. Types of Top-Down Parser

In this section, we will be discussing various forms of top-down parsing. The most general form of top-down parsing is recursive descent parsing.

We can perform recursive descent parsing in two ways:

1. One which requires backtracking.
2. Other which requires no backtracking.

The method that doesn’t need backtracking is referred to as predictive parsing. The figure below illustrates various forms of top-down parsing.

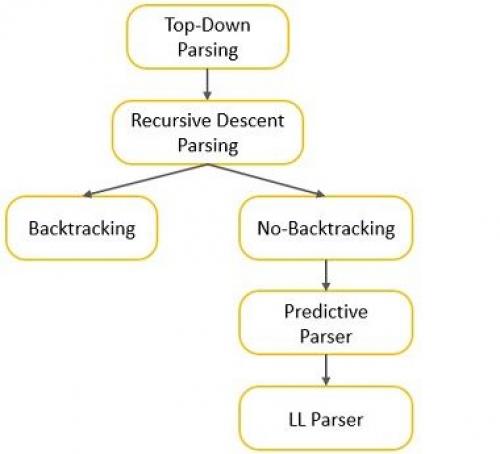
Recursive Descent Parsing

A recursive descent parsing program has a set of procedures. There is one procedure for each of the non-terminal present in the grammar. The parsing starts with the execution of the procedure meant for the starting symbol.

void A() { 1)            Choose an A-production, A-> X1 X2 … Xk; 2)            for (i = 1 to k) { 3)                   if (Xi is a nonterminal) 4)                             call procedure Xi(); 5)                   else if (Xi = current input symbol a) 6)                   advance the input to the next symbol; 7)                   else /* an error has occurred */; } }

The pseudocode above expresses the procedure for a typical non-terminal. This pseudocode is non-deterministic. This is because it doesn’t specify the method in which the production of a non-terminal must be applied.